Quod erat demonstrandum

von Femke Sporn

Um die Frage, ob das mathematische Beweisverständnis gezielt gefördert werden kann, zu beantworten, wurde am IPN ein theoretisches Rahmenmodell für das mathematische Beweisverständnis von Lernenden entwickelt. Basierend auf diesem Modell wurde das Beweisverständnis von Lernenden vor und nach einer Intervention untersucht.

Mathematisches Beweisen ist die Methode, mit der in der Mathematik Evidenz generiert wird. Mit mathematischen Beweisen werden Aussagen und Regeln in der Mathematik abgesichert und neue Erkenntnisse gewonnen. Nicht ohne Grund sind mathematische Beweise daher Thema des Mathematikunterrichts der Sekundarstufe und sie kommen in vereinfachter Form bereits in der Grundschule im Zuge des mathematischen Argumentierens vor. Ein Mathematikunterricht ohne die Erwähnung des Beweisens wäre vergleichbar mit einem Chemie- oder Physikunterricht ohne Experimente – ein wesentlicher Aspekt des Faches würde fehlen. Neben dem Erwerb bestimmter mathematischer Fähigkeiten ist es deshalb wichtig, dass Lernende die Mathematik als beweisende Disziplin kennenlernen.

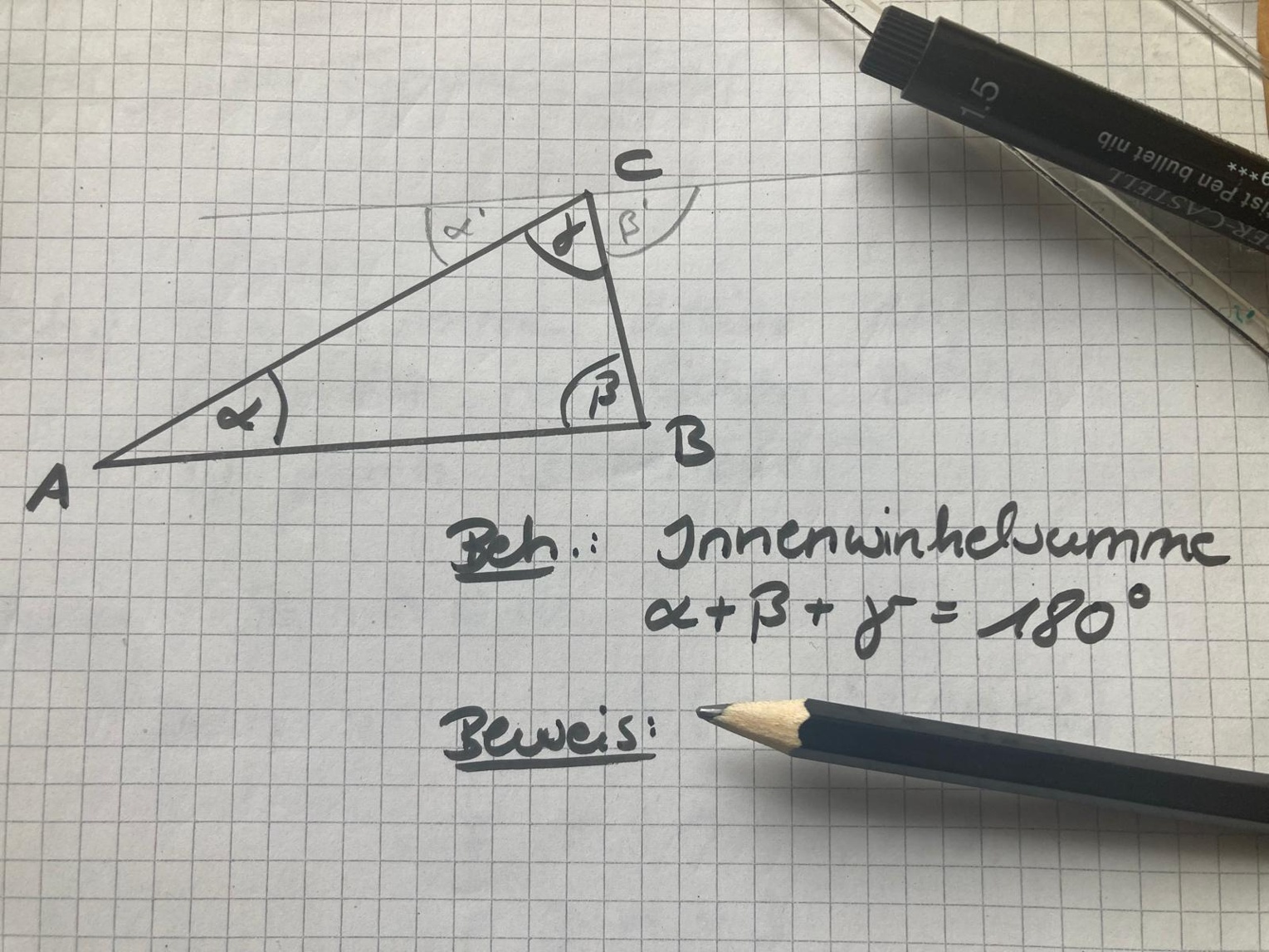
Im Laufe ihrer Schulzeit setzen sich Schüler*innen wiederholt mit mathematischen Beweisen auseinander. In Deutschland geschieht dies vor allem von der siebten Klassenstufe an im Geometrieunterricht (anhand des Innenwinkelsummensatzes oder des Satzes des Pythagoras).

Entwicklung eines theoretischen Modells für das Beweisverständnis

Indem sich Lernende wiederholt mit dem mathematischen Beweisen beschäftigen, sollten sie ein Beweisverständnis aufbauen und es ist zu vermuten, dass sich dieses über die Zeit entwickelt. Ein Beweisverständnis umfasst, dass Lernende das Konzept von Beweisen, ihre Funktionen, Regeln und Prinzipien und ihre Bedeutung für die Mathematik verstehen. Ein solches Beweisverständnis ist mit einem Verständnis der Rolle des Experimentierens im Fach Chemie oder Physik vergleichbar.

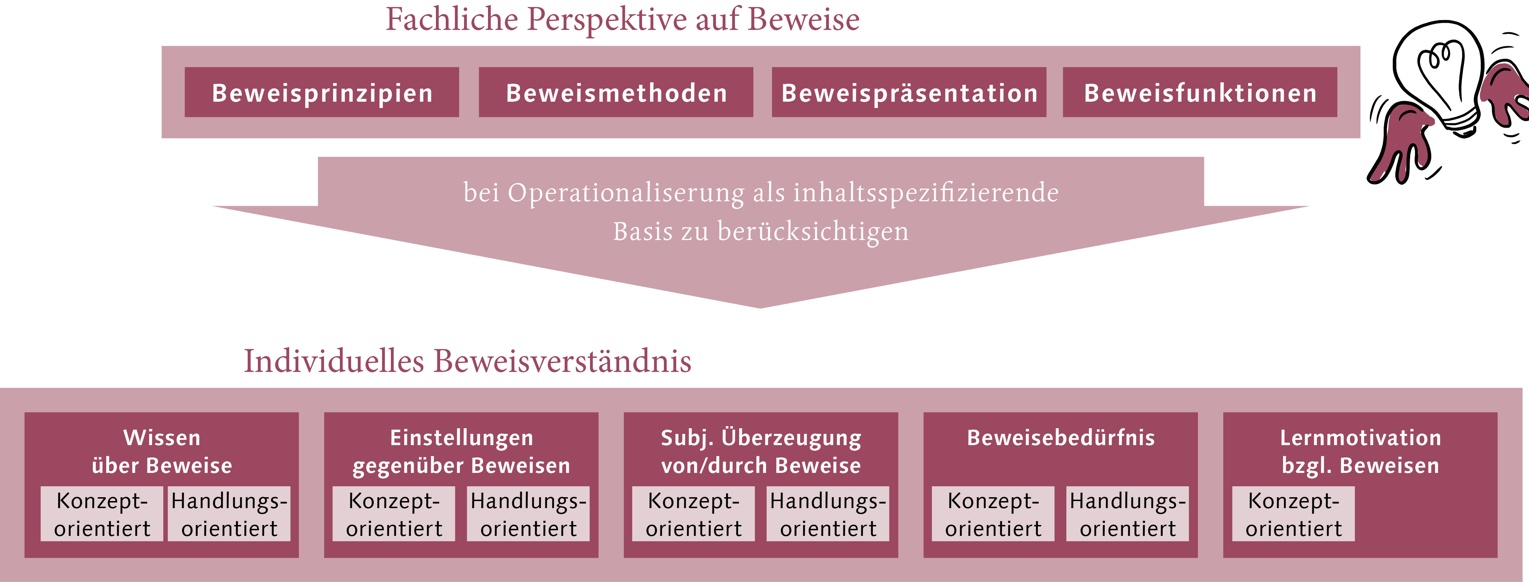
Ein Blick in die bisherige Forschung zeigt jedoch, dass es keine einheitliche Definition für dieses Beweisverständnis gibt. Daher konnte bisher weder das Beweisverständnis von Lernenden noch seine Entwicklung systematisch untersucht werden. Um diese Forschungslücke zu schließen, wurde zunächst ein theoretisches Rahmenmodell für das Beweisverständnis entwickelt, das verschiedene Aspekte und Unterscheidungen der bisherigen Forschung integriert. Mit diesem Modell lassen sich Erkenntnisse bisheriger Forschung systematisieren und es entsteht eine einheitliche Grundlage für zukünftige Forschung. Zentrale Unterscheidungen im Modell sind beispielsweise die fachliche Perspektive auf Beweise und das individuelle Beweisverständnis sowie der konzept- und handlungsorientierte Fokus des individuellen Beweisverständnisses.

Beweisverständnis im Verlauf der mathematischen Ausbildung

Das theoretische Rahmenmodell machte es möglich, das Beweisverständnis von Lernenden zu messen, d. h. es wurde eine Vielzahl an Aufgaben und Fragen entwickelt, um die verschiedenen Aspekte des Beweisverständnisses zu erfassen. Zwei empirische Studien zur Untersuchung des Beweisverständnisses von Lernenden konnten auf dieser Grundlage durchgeführt werden: eine Querschnittsstudie mit Studienanfänger*innen der Mathematik (Studie 1) und eine quasi-längsschnittliche Studie mit Schüler*innen (Studie 2).

Die Ergebnisse zeigen, dass das Beweisverständnis von Schüler*innen gering ausgeprägt ist und sich während Schulzeit – entgegen der Erwartung – kaum entwickelt. Die Schüler*innen der Klassenstufen 8 bis 11 hatten Schwierigkeiten, Kriterien für gültige Beweise anzugeben. So erkannten etwa 85% der Schülerinnen und Schüler nicht, dass fünf konkrete Beispiele nicht ausreichen, um die Aussage „Die Summe von drei aufeinanderfolgenden natürlichen Zahlen ist durch 3 teilbar“ allgemeingültig zu beweisen. Auch die Studienanfänger*innen wiesen Verständnisschwierigkeiten auf, wenngleich sie ein etwas höheres Beweisverständnis als die Schüler*innen zeigten. Da es sich bei den Mathematikstudierenden um eine positiv selektierte Gruppe handelt, ist dieses Ergebnis jedoch zu relativieren.

Insgesamt deuten beide Studien darauf hin, dass sich das Beweisverständnis der Lernenden während der Schulzeit kaum positiv entwickelt – obwohl sie sich im Mathematikunterricht regelmäßig mit mathematischen Beweisen auseinandersetzen. Zwar liefern die Studien keine detaillierten Informationen zu den Lerngelegenheiten, die die Lernenden erhielten, jedoch legen die Ergebnisse nahe, dass die aktuellen Lerngelegenheiten nicht ausreichen.

Gezielte Förderung des Beweisverständnisses

Angesichts der eher geringen Ausprägung des Beweisverständnisses stellte sich die Frage, ob eine gezielte Förderung möglich ist. Im Rahmen einer quasi-experimentellen Interventionsstudie (Studie 3) wurde daher eine Lernumgebung entwickelt, die vielfältige Lerngelegenheiten zum mathematischen Beweisen für die neunte Klassenstufe bietet. Die Intervention besteht aus fünf Unterrichtsstunden, die, über ein Schulhalbjahr verteilt, in den regulären Mathematikunterricht integriert werden können. Die entwickelten Lerngelegenheiten schließen an Inhalte an, die ohnehin für den Mathematikunterricht vorgesehen sind, wobei ein besonderer Fokus auf Reflexion und Diskussion über Beweise gelegt wurde. Die Schüler*innen sollen beispielsweise anhand nicht akzeptabler Beweisversuche erarbeiten, dass eine Argumentation mit noch nicht bewiesenen Aussagen keinen gültigen mathematischen Beweis darstellen kann. Zusätzlich werden Kriterien für Beweise explizit formuliert und auf einem Plakat über die gesamte Intervention hinweg gesichert.

Im Rahmen der Studie wurde das Beweisverständnis der Schüler*innen vor und nach der Intervention untersucht und mit dem Beweisverständnis einer Kontrollgruppe verglichen, die nicht an der Intervention teilnahm. Die Ergebnisse zeigen, dass die entwickelten Lerngelegenheiten wenigstens einzelne Aspekte des Beweisverständnisses stärken konnten. So verbesserten sich die Lernenden bei der Validierung fehlerhafter Beweisversuche. Allerdings bleibt das Beweisverständnis auch nach der Intervention unter dem Niveau, das aus fachlicher Sicht wünschenswert wäre.

Fazit

Die hier vorgestellten Studien geben Einblick in das Beweisverständnis von Lernenden und dessen Entwicklung im Verlauf ihrer mathematischen Ausbildung. Die Ergebnisse der beiden ersten Studien legen nahe, eine gezielte Förderung des Beweisverständnisses auch in weiteren Klassenstufen zu integrieren. Basierend auf diesen Ergebnissen sollen daher nun weitere Materialien für den Unterricht von der siebten Klassenstufe an entwickelt und erprobt werden, um zu untersuchen, ob eine regelmäßige gezielte Förderung des Beweisverständnisses zu langfristigen Verbesserungen führen kann.

Über die Autorin:

Dr. Femke Sporn ist am IPN wissenschaftliche Mitarbeiterin in der Abteilung Didaktik der Mathematik. Sie studierte Mathematik und Biologie auf Lehramt an Gymnasien an der Christian-Albrechts-Universität zu Kiel. Die hier vorgestellten Ergebnisse basieren auf Teilen ihrer am IPN angefertigten Dissertation.

Weiterführende Literatur:

Sporn, F., Sommerhoff, D., & Heinze, A. (2021). Beginning university mathematics students' proof understanding. In M. Inprasitha, N. Changsri, & N. Boonsena (Hrsg.), Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education (S. 105-112). PME.

Sporn, F., Sommerhoff, D., & Heinze, A. (2022). Students' Knowledge About Proof and Handling Proof. In C. Fernández, S. Llinares, Á. Gutiérrez, & N. Planas (Hrsg.), Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education (S.27-34), PME.

Sporn, F., Sommerhoff, D., & Heinze, A. (2023). Fostering students' knowledge about proof. In M. Ayalon, B. Koichu, R. Leikin, L. Rubel, & M. Tabach (Hrsg.), Proceedings of the 46th Conference of the International Group for the Psychology of Mathematics Education (S. 235-242). PME.